Answer:
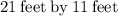
Explanation:
(Assuming the den is a rectangle)
Let
 be the length of the den. Because the length is 10 feet longer than the width, the width of the den can be represented as
be the length of the den. Because the length is 10 feet longer than the width, the width of the den can be represented as
 .
.
The area of a rectangle is given as
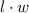 , therefore we can form the following equation:
, therefore we can form the following equation:
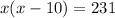
Expanding this, we have:

This factors into
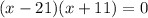 , therefore
, therefore
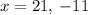 .
.
Because -11 is extraneous, the length of the den is
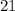 feet and the width is
feet and the width is
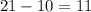 . Thus, the dimensions of the den are
. Thus, the dimensions of the den are
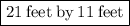 .
.