Question

What can you say about the sum of consecutive odd numbers starting with 1? that is, evaluate 1, 1c3, 1c3c5, 1c3c5c7, and so on, and formulate a conjecture?

Answer 1

Let us add consecutive odd numbers and try to find any relationship.

1. 1

2. 1+3 = 4 ( square of 2 i.e
`2^(2)` )

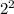3. 1+3+5 = 9 (
`3^(2)` )

4. 1+3+5+7 = 16 (
`4^(2)` )

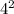5. 1+3+5+7+9 = 25 (
`5^(2)` )

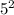6. 1+3+5+7+9+11 = 36 (
`6^(2)` )

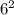7. 1+3+5+7+9+11+13 = 49 (
`7^(2)` )

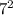If we notice, the sum of the consecutive odd integers in each case is equal to the square of the place where it lies. For example, the sum of numbers in seventh place is equal to
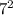`7^(2)`. The sum of the numbers in the fifth line is equal to
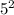`5^(2)`.