Question

Calculate the pH for the following weak acid.

A solution of HCOOH has 0.14M HCOOH at equilibrium. The Ka for HCOOH is 1.8×10−4. What is the pH of this solution at equilibrium?

Express the pH numerically.

Answer 1

Answer:- pH of the solution is 2.30.

Solution:- The ionization equation for the given acid is written as:

`HCOOH\leftrightarrow H^++HCOO^-`

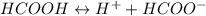
Let's say the initial concentration of the acid is c and the change in concentration x.

Then, equilibrium concentration of acid = (c-x)

and the equilibrium concentration for each of the product would be x.

Equilibrium expression for the above equation would be:

`Ka=([H^+][HCOO^-])/([HCOOH])`

`1.8*10^-^4=(x^2)/(c-x)`

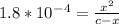
From given info, equilibrium concentration of the acid is 0.14.

So, (c-x) = 0.14

hence,
`1.8*10^-^4=(x^2)/(0.14)`

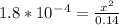
Let's solve this for x. Multiply both sides by 0.14.

`2.52*10^-^5=x^2`

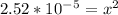
taking square root to both sides:

`x=0.00502`

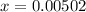
Now, we have got the concentration of
`[H^+]` .

`[H^+]` = 0.00502 M

We know that,
`pH=-log[H^+]`

pH = -log(0.00502)

pH = 2.30

So, the pH of HCOOH solution is 2.30.