Question

Let’s explore a quotient raised to an exponent

Answer 1

You can think of exponents as abbreviations for repeated multiplication. By that definition:

`\big((6)/(y)\big) ^3 =(6)/(y) *(6)/(y) *(6)/(y)`

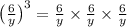
Which, by the properties of fraction multiplication, is the same thing as

`(6*6*6)/(y* y* y)`

whiiiich, going back to our abbreviations, is the same thing as

`(6^3)/(y^3)`

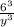
And since 6³ = 216, our final simplified answer is

`(216)/(y^3)`

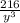
The most important discovery in this problem is the property that

`\big( (x)/(y)\big)^n=(x^n)/(y^n)`

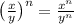
You could almost say that the exponent gets "distributed" to the numerator and denominator, and in fact, any exponents will have this property of "distributing" across multiplication or division.

Answer 2

The answer is 216/y^3