Question

Find the minimum value of the function f(x) = x2 + 5x – 6

Answer 1

So the easiest method to find the vertex (the minimum in this case) to do this is to find the axis of symmetry, then plug it into the function.

Firstly, the equation to find the axis of symmetry is
`x=(-b)/(2a)` , with b = x coefficient and a = x^2 coefficient. The equation equation can be solved as such:

`x=(-5)/(2*1)\\\\x=(-5)/(2)\\\\x=-2.5`

Since the vertex falls on the axis of symmetry, we know that the x-coordinate of the vertex is -2.5. Now to solve for the y-coordinate, plug in x with -2.5 and solve as such:

`f(-2.5)=(-2.5)^2+5*(-2.5)-6\\ f(-2.5)=6.25+(-12.5)-6\\ f(-2.5)=-12.25`

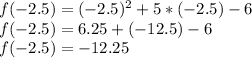
Now putting it all together, our minimum value (vertex) is (-2.5,-12.25).