Question

Mr. Mole left his burrow and started digging his way down.

A(t)A(t)A, left parenthesis, t, right parenthesis models Mr. Mole's altitude relative to the ground (in meters) after ttt minutes.
A(t)=-2.3t-7A(t)=−2.3t−7A, left parenthesis, t, right parenthesis, equals, minus, 2, point, 3, t, minus, 7
How fast did Mr. Mole descend?

Answer 1

2.3 meters per minute

Explanation:

I got it right on khan

Answer 2

Mr. Mole descends 2.3 meters per minute.

Step by step explanation:

We have been given a function:
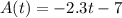`A(t)=-2.3t-7`, which models Mr. Mole's altitude relative to the ground (in meters) after t minutes. We are asked to find how fast Mr. mole descend.

We can see that at time equals 0 minutes, Mr. Mole's altitude is 7 meters below the ground, so -7 represents y-intercept.

We can also see that slope of our given function is -2.3, which represents change in Mr. Mole's altitude with respect to time in minutes. Since our slope is negative, so Mr. Mole's altitude is descending by 2.3 meters per minute.

Therefore, Mr. Mole is descending by 2.3 meters per minute.