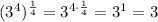Question

Find the indicated real n roots of a

N=4, a=81

Answer 1

`81|3\\27|3\\.\ 9|3\\.\ 3|3\\.\ 1|\\\\81=\underbrace{3\cdot3\cdot3\cdot3}_(4)=3^4\\\\\sqrt[4]{81}=\sqrt[4]{3^4}=3\\\\Used:\\\sqrt[n]{a^n}=a`

Answer 2

If I understood coorectly, you're looking for the fourth root of 81. This exercise can be solved by remembering that extracting the fourth root of a number is the same as raising that number to the power of 1/4.

We also need the prime factorization of 81, which is

`81 = 9 * 9 = 3^2 * 3^2 = 3^4`

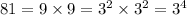
So, the fourth root of 81 is 81 raised to the power of 1/4, which means

`\sqrt[4]{81} = \sqrt[4]{3^4} = (3^4)^{(1)/(4)}`

Now, use the property of exponents
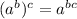`(a^b)^c = a^(bc)` to convert the expression into

`(3^4)^{(1)/(4)} = 3^{4\cdot (1)/(4)} = 3^1 = 3`