If (4x^2y^2 + 8x^3y^5)/(2xy^2) is completely simplified to 2x^ay^b + 4x^cy^d, where a, b, c, and d represent integer exponents, what is the value of c?

Question

If
`(4x^2y^2 + 8x^3y^5)/(2xy^2)` is completely simplified to
`2x^ay^b + 4x^cy^d`, where a, b, c, and d represent integer exponents, what is the value of c?

Answer 1

`\frac{4 {x}^(2) {y}^(2) + 8 {x}^(3) {y}^(5) }{2x {y}^(2) } \\ = \frac{4 {x}^(2) {y}^(2) }{2 x {y}^(2) } + \frac{8 {x}^(3) {y}^(5) }{2x {y}^(2) } \\ = 2 {x}^(2 - 1) {y}^(2 - 2) + 4 {x}^(3 - 1) {y}^(5 - 2) \\ = 2 {x}^(1) {y}^(0) + 4 {x}^(2) {y}^(3)`
C=2

Answer 2

First of all, thanks for properly formatting the question!! That's something you don't see so often..

Anyway, the first thing to do is split the fraction in two fractions, using the rule

`(a+b)/(c) = (a)/(c)+(b)/(c)`

So, your expression becomes

`(4x^2y^2+8x^3y^5)/(2xy^2) = (4x^2y^2)/(2xy^2)+(8x^3y^5)/(2xy^2)`

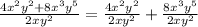
Now, for each of the fractions we can simplify the numeric part and the exponents, using the rule

`(x^a)/(x^b) = x^(a-b)`.

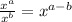We have

`(4x^2y^2)/(2xy^2) = 2x`

`(8x^3y^5)/(2xy^2) = 4x^2y^3`

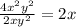
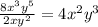
So, the whole expression becomes

`2x+4x^2y^3`

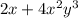
which means that the four coefficients are

`a=1, b=0, c=2, d=3`

So, in particular, c=2