Question

PLEASEEE HURRRY!!!!!!!

Law of sines: What is the approximate perimeter of the triangle? Use the law of sines to find the answer.
A.  4.6 units
B. 5.7 units
C. 6.9 units
D. 9.2 units

Answer 1

the answer is D 9.2 units

Answer 2

Option D. 9.2 units.

Explanation:

In the ΔJKL ⇒ ∠J + ∠K + ∠L = 180

∠J + 67 + 74 = 180° ⇒ ∠J = 39°

In the given triangle JKL we apply law of sines

`(SinK)/(JL)` =
`(SinJ)/(KL)` =
`(SinL)/(JK)`

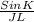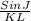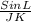
Now we take
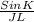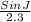
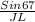`(SinK)/(JL)` =
`(SinJ)/(2.3)`

`(Sin67)/(JL)` =
`(Sin39*)/(2.3)`

JL =
`((2.3)Sin67)/(Sin39)`

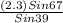
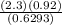`((2.3)(0.92))/((0.6293))` = 3.36 units

Now
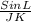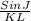
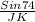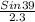
`(SinL)/(JK)` =
`(SinJ)/(KL)`

`(Sin74)/(JK)` =
`(Sin39)/(2.3)`

JK =
`(2.3(Sin74))/((Sin39))`

=
`(2.3(0.9613))/((0.6293))`

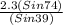
= 3.51 units

So perimeter of the triangle = 3.36 + 3.51 + 2.3 = 9.15 units ≈ 9.2 units.

Option D is the answer.