Question

I’m confused on this one

Answer 1

I think its 90 degrees. 

Answer 2

I like incenter problems but this one looks underdetermined. Is there enough information to get anywhere? We're given what, an isoscleles triangle perhaps, with a common side of AC=BC=37?

The incenter is the center of the inscribed circle, which will be tangent to all the sides, so each radius to the points where the circle touches the triangle will be perpendicular to the side. The three radii are concurrent, their meet the incenter, the center of the incircle, oddly called G here.

(For the record, standard notation is centroid G, orthocenter H, circumcenter O, incenter I, Nine Point Center N.)

r=EG=FG=DG is the altitude of three triangles that make up the whole triangle. If we call a=BC, b=AC, c=AB we have equal areas:


`\frac 1 2 ar + \frac 1 2 b r + \frac 1 2 c r = \textrm{area ABC}`


`\frac r 2 (a+b+c) = \textrm{area ABC}`


`r = \frac{ \textrm{area ABC}}{\frac 1 2 (a+b+c)}`

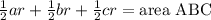
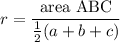
We can plug in Heron's formula for the area; the denominator is already the semiperimeter.

But that doesn't really get us anywhere as we only know one side, perhaps two if we assume the triangle is isosceles but not the third.