Question

5.1.) Find the answer to:

Answer 1

To derive this function, we'll only need the power rule.

Power rule is expressed with the following function:


`(d)/(dx) x^n = n \cdot x^(n-1)`

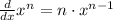
We can derive each of the terms individually. Rewrite the problem:


`(d)/(dx) [(1)/(√(x)) - 3.2x^(-2) + x] = ((d)/(dx) (1)/(√(x))) - ((d)/(dx) 3.2x^(-2)) + ((d)/(dx) x)`

For the first term, we'll rewrite the term, then use the power rule (note that square roots can be rewritten as any number to the 1/2 power):


`(d)/(dx) (1)/(√(x)) = (d)/(dx) x^{-(1)/(2)} = -(1)/(2) x^{-(3)/(2)} = -\frac{1}{2x^{(3)/(2)}}`

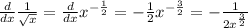
For the second term, we'll use power rule:


`(d)/(dx) 3.2x^(-2) = -6.4x^(-3) = -(6.4)/(x^3) = -(32)/(5x^3)`

The third term is simple:


`(d)/(dx) x = 1`

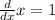
The equation should now look like this, and result in your answer:


`(d)/(dx) [(1)/(√(x)) - 3.2x^(-2) + x] = -\frac{1}{2x^{(3)/(2)}} - (-(32)/(5x^3)) + 1 = \boxed{-\frac{1}{2x^{(3)/(2)}} + (32)/(5x^3) + 1}`