Question

Determine if ƒ(x) = 3x2 – 2x3 – x – 9 is a polynomial function. If it is, state the degree and the leading coefficient. If not, state why.

Answer 1

This is indeed a polymomial, it's just not in the correct order. The term with the highest exponent goes first, dictating the degree of the whole entire polynomial. In descending order, the polynomial is written correctly as
`-2x^3+3x^2-x-9`. It is a third degree polynomial with a leading coefficient of -2.

Answer 2

Answer: The given function is a polynomial function with leading coefficient -2.

Step-by-step explanation: We are given to determine whether the following function is a polynomial function :

`f(x)=3x^2-2x^3-x-9.`

If yes, we are to state the degree and the leading coefficient. If not, we are to state the reason.

We know that

any polynomial function is of the form :

`p(x)=a_nx^n+a_(n-1)x^(n-1)+a_(n-2)x^(n-2)+~~.~~.~~.~~+a_1x+a_0,`

with degree n.

Son according to this definition, the given function f(x) is a polynomial function with degree 3.

The standard form of the given polynomial function is:

`f(x)=-2x^3+3x^2-x-9.`

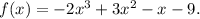
Since the leading coefficient is the coefficient of the highest power of x, so the leading coefficient is -2.

Thus, the given function is a polynomial function with leading coefficient -2.