Question

The locations, given in polar coordinates, for two ships are (8 mi, 63º) and (8 mi, 123º). Find the distance between the two ships.

Answer 1

A

Step-by-step explanation: believe me or not i dont really care

Answer 2

we know that

The arrangement forms an isosceles triangle with equal legs of 8 miles.
The angle between the legs is equal to


`123-63=60`°

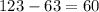
Therefore, the other two angles are
Angles = (180-60)/2 = 120/2 = 60°
It can, therefore, be noted that all angles are equal and thus the resulting triangle is actually an equilateral triangle and thus all the sides are equal.

Hence
the answer is
the distance between the two ships is 8 miles apart

alternative Method
Applying the law of cosines
c²=a²+b²-2*a*b*cos C
where
a=8 miles
b=8 miles
C is the angle between the legs-------> 123-63------> 60 degrees
c is the distance between the two ships
so
c²=8²+8²-2*8*8*cos 60------> c²=64-------> c=√64------> c=8 miles