From our graph we can infer that the our function intercept the x-axis at the points
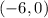
and

. Notice that bellow those two points our function is negative, whereas above those two points our function is positive. In other words:
the function is positive for all real values of

where
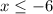
or
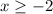
, and the function is negative for all real values of

where
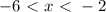
We can conclude that the correct answer is:
The function is negative for all real values of x where –6 < x < –2.