Question

find x. assume that segments that appear tangent are tangent. please help need answer and how to do it.

Answer 1

a^2+b^2=c^2

16^2+b^2=20^2

256+b^2=400

b^2=144

square root of 144=12

x=12

Explanation:

Answer 2

Triangle ABC is a right triangle, meaning we can use the Pythagorean Theorem to find x.
The formula for the Pythagorean Theorem is:

`a = \sqrt{ {b}^(2) + {c}^(2) }`
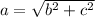
where a is the hypotenuse, and b and c are the legs.
In this problem, we have the vertical leg as 16, the horizontal leg as x, and the hypotenuse as 20. Therefore, we can say that

`a = 20 \\ b = 16 \\ c = x`
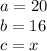
Therefore, we can plug into the formula to find x:
`a = \sqrt{ {b}^(2) + {x}^(2) } \\ {a}^(2) = { \sqrt{ {b}^(2) + {x}^(2) } }^(2) \\ {a}^(2) = {b}^(2) + {x}^(2) \\ {a}^(2) - {b}^(2) = {x}^(2)`
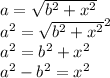
We first change the variable c to x and square both sides of the equation. Then we subtract b^2 from both sides.

`{x}^(2) = {a}^(2) - {b}^(2) \\ \sqrt{ {x}^(2) } = \sqrt{ {a}^(2) - {b}^(2) } \\ x = \sqrt{ {a}^(2) - {b}^(2) }`
We square root each side to find the variable answer for x. Then we plug in the numbers:
`x = \sqrt{ {(20)}^(2) - {(16)}^(2) } \\ x = √(400 - 256) \\ x = √(144) \\ x = 12`
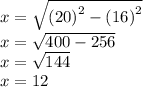
We find that x = 12. The answer is A. 12.