Question

The formula s= SA/6 squared gives the length of the side, s, of a cube with a surface area, SA. How much longer is the side of a cube with a surface area of 1,200 square inches than a cube with the surface area of 768 square inches?

Answer 1

The surface area (SA) of a cube can be written as:

SA = 6s²

From here we can write, the length of the side s as:


`s= \sqrt{ (SA)/(6) }`

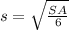
For cube with surface area of 1200 square inches, the side length will be:


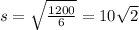
`s= \sqrt{ (1200)/(6) }=10 √(2)` inches

For cube with surface area 768 square inches, the side length will be:


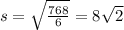
`s= \sqrt{ (768)/(6) }=8 √(2)` inches

The difference in side lengths of two cubes will be:


`10 √(2) -8 √(2)=2 √(2)`

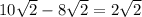Rounding to nearest tenth of an integer, the difference between the side lengths of two cubes will be 2.8 inches.