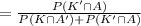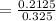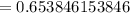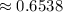Question

We now know that the test predicted that Kevin does not have the disease. Using this information, calculate the probability that Kevin does not have diabetes after the test was taken.Kevin’s family has a history of diabetes. The probability that Kevin would inherit this disease is 0.75. Kevin decides to take a test to check if he has the disease. The accuracy of this test is 0.85.

Answer 1

To get the intersection of the both event you can simply multiply the both events because those two events are independent to each other so the formula would be (0.75) time (0.85) and the probability would be 0.6375.

Answer 2

0.6538 ( approx )

Explanation:

Suppose K shows that kevin has disease,

K' shows that he does not have the disease,

A shows that the test is accurate,

A' shows that test is inaccurate,

According to the question,

P(K) = 0.75 ⇒ P(K') = 1 - P(K) = 0.25,

P(A) = 0.85 ⇒ P(A') = 1 - P(A) = 0.15,

Thus, the probability that kelvin has diseases if test is inaccurate,

P(K∩A') = P(K) × P(A') = 0.75 × 0.15 = 0.1125,

Also, the probability that kelvin does not have disease if the test is accurate,

P(K'∩A) = P(K') × P(A) = 0.25 × 0.85 = 0.2125,

So, the probability that test is negative = P(K∩A') + P(K'∩A)

= 0.1125 + 0.2125

= 0.325.

Hence, the probability that Kevin does not have diabetes if the test predicted that Kevin does not have the disease

`=(P(K'\cap A))/( P(K\cap A') + P(K'\cap A))`

`=(0.2125)/(0.325)`

`=0.653846153846`

`\approx 0.6538`