Answer:
Total money earned on Thursday is $1090.
Explanation:
Let amount of money for one house call of Plumber A be x
So, amount of money for 2 house call of Plumber A=2 x
So, amount of money for 4 house call of Plumber A=4 x
So, amount of money for 3 house call of Plumber A=3 x
Let amount of money for one house call of Plumber B be y
So, amount of money for 8 house call of Plumber B=8 y
So, amount of money for 7 house call of Plumber B=7 y
So, amount of money for 9 house call of Plumber B=9 y
Let amount of money for one house call of Plumber C be z
So, amount of money for 8 house call of Plumber C=8 z
So, amount of money for 10 house call of Plumber C=10 z
So, amount of money for 9 house call of Plumber C=9 z
Now we are given that The total amount of money earned by all three plumbers on Monday was $1,400.
On Monday Plumber A has 2 calls , Plumber B has 8 calls and Plumber C has 8 calls
So, equation becomes:
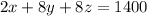 --1
--1
On Tuesday they earned a total of $1,660,On Tuesday Plumber A has 4 calls , Plumber B has 7 calls and Plumber C has 10 calls.
So, equation becomes:
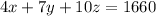 ---2
---2
On Wednesday, they earned a total of $1,650.On Wednesday Plumber A has 3 calls , Plumber B has 9 calls and Plumber C has 9 calls.
So, equation becomes:
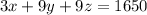 ----3
----3
Solving equation 1 ,2 AND 3
Equation 3:
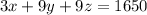
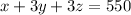 ---4
---4
Now substitute the value of x from 4 in 1 and 2
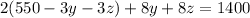 and
and
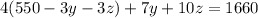
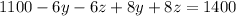 and
and
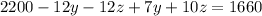
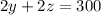 --- (a) and
--- (a) and
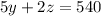 ---(b)
---(b)
Now substitute the value of y from a in b
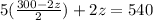
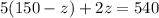
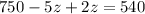
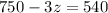
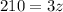
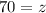
Substitute the value of z in (a)
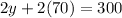
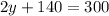
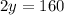
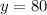
Substitute the value of y and z in 1
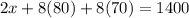
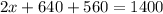
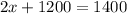
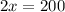
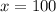
So, amount of money for one house call of Plumber A = $100
So, amount of money for one house call of Plumber B =$80
So, amount of money for one house call of Plumber C =$70
On Thursday Plumber A made four house calls, Plumber B made six house calls, and Plumber C made three house calls.
So, equation becomes :
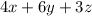
Substitute the values of x ,y and z
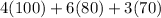
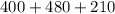
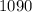
Thus total money earned on Thursday is $1090.
Hence Option C is correct.