Answer with explanation:
It is given that ,Marge correctly guessed whether a fair coin turned up "heads" or "tails" on sic consecutive flips.
When we flip a coin , there are two possible Outcomes, one is Head and another one is Tail , that is total of 2.
Probability of an event

Probability of getting head
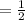
Probability of getting tail
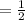
⇒There can be two guesses , either it will be true and another one will be false.
So, Possible outcome of correct guess={True, False}=2
--Probability of Incorrect(False) guess
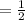
--Probability of Correct(True) guess in seventh toss
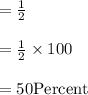
⇒Probability that she will correctly guess the outcome of the Seventh coin toss, if previous sixth tosses has correct guess
=T×T×T×T×T×T×T, where T=True guess
= 0.5×0.5×0.5×0.5×0.5×0.5×0.5
=0.0078125
=0.0078 (approx)