Answer:
The integral is equal to
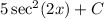 for an arbitrary constant C.
for an arbitrary constant C.
Explanation:
a) If
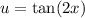 then
then
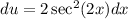 so the integral becomes
so the integral becomes
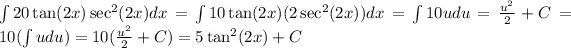 . (the constant of integration is actually 5C, but this doesn't affect the result when taking derivatives, so we still denote it by C)
. (the constant of integration is actually 5C, but this doesn't affect the result when taking derivatives, so we still denote it by C)
b) In this case
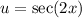 hence
hence
 . We rewrite the integral as
. We rewrite the integral as
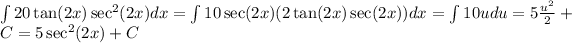 .
.
c) We use the trigonometric identity
 is part b). The value of the integral is
is part b). The value of the integral is
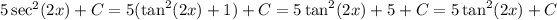 . which coincides with part a)
. which coincides with part a)
Note that we just replaced 5+C by C. This is because we are asked for an indefinite integral. Each value of C defines a unique antiderivative, but we are not interested in specific values of C as this integral is the family of all antiderivatives. Part a) and b) don't coincide for specific values of C (they would if we were working with a definite integral), but they do represent the same family of functions.