Answer:
θ = 4.1 rev
Step-by-step explanation:
For this problem we can use the relationship of rotational kinematics
w = θ / t
θ = w t
Angular and linear variables are related.
v = w r
w = v/r
θ = (v / r) t (1)
We see that we must find the linear velocity and the radius of the orbit, let's use Bohr modeling
The radius of the orbit
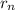 = a₀ n²
= a₀ n²
a₀ = 0.0529 nm
For our case
n = 3
r₃ = 0.0529 3²
r₃ = 0.4761 nm
The energy of the atomic level is
Eₙ = -13.606 / n²
n = 3
E₃ = -13.606 / 3²
E₃ = -1.512 eV
Let's reduce to July
E₃ = -1.512 eV (1.6 10⁻¹⁹ J / 1 eV) = 2.4192 10⁻¹⁹ J
Let's use mechanical energy is
E = K + U
E = ½ m v² - k e² / r
v² = (E + k e² /r) 2/m
v² = (2.4192 10⁻¹⁹ + 8.99 10⁹ (1.6 10⁻¹⁹)² /0.4761 10-⁻⁹) 2/9.1 10⁻³¹
v² = (2.4192 10⁻¹⁹ + 4.8339 10⁻¹⁹) 0.2198 10³¹
v² = 1.5942 10¹²
v = 1.23 10⁶ m / s
Let's replace in equation 1
θ = v t / r
θ = 1.23 10⁶ 10⁻⁸ / 0.4761 10⁻⁹
θ = 2.5835 10¹ rad
Let's reduce revolutions
θ = 25,835 rad (1 rev / 2π rad)
θ = 4.1 rev