Question

Consider the paraboloid surface z = x 2 + y 2 .

a. (3 points) Find the equation of the plane tangent to the surface at (1, 1, 2).
b. (7 points) Find the equation of the plane which is tangent to the paraboloid surface and contains the line (x, y, z) = (t, 2 − 2t, −1).

Answer 1

a. We don't really need calculus to do this

`z = f(x,y) = x^2 + y^2`

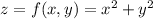
We're interested in f near (1,1,f(1,1))

`f(x,y)=f(1+(x-1), 1+(y-1)) = (1+(x-1))^2 + (1+(y-1))^2`

`f(x,y)=2 + 2(x-1) + 2(y-1) + (x-1)^2 + (y-1)^2`

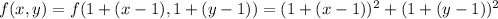
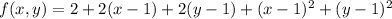
The tangent plane at (1,1,2) is the best linear approximation to f at (1,1). We just drop the squared terms:

`z =2 + 2(x-1) + 2(y-1)`

`z=2x + 2y - 2`

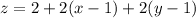
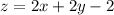
Answer: 2x + 2y - z = 2

b.

We repeat the above in general, near f(r,s)

`f(x,y)=f(r + (x-r), s+(x-s))`

`f(x,y) = (r + (x-r))^2 + (s + (x-s))^2`

`f(x,y)= r^2 + s^2 + 2r(x-r) + 2s(y-s) + (x-r)^2 + (y-s)^2`

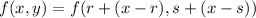
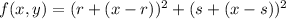
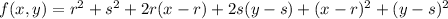
Again the tangent plane at (r,s,f(r,s)) is gotten by dropping the squared terms,

`z = r^2 + s^2 + 2r(x-r) + 2s(y-s)`

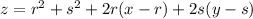
This has to contain

`(x,y,z)=(t, 2-2t, -1)=(0,2,-1) + t(1,-2,0)`

`-1 = r^2 + s^2 + 2r(0-r) + 2s(2-s)`

`r^2 + s^2 - 4s - 1 = 0`

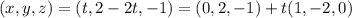
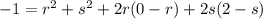
The line is perpendicular to the normal of the plane, so a zero dot product.

`2r x + 2sy - z = r^2 + s^2`

`(2r, 2s, -1) \cdot (1, -2, 0) = 0`

`2r - 4s=0`

`r = 2s`

`(2s)^2 + s^2 - 4s -1=0`

`5s^2 - 4s -1 = 0`

`(5s + 1)(s - 1) = 0`

`s=1 \textrm{ or } s=-1/5`

`r=2, s=1 \textrm{ or } r=-2/5, s=-1/5`

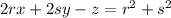
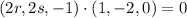
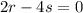
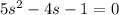
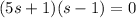
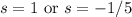
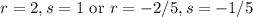
Two tangent planes contain the line.

`2r x + 2sy - z = r^2 + s^2`

`4x + 2y - z = 5 \textrm{ and } (-4/5)x - (2/5)y - z = (-2/5)^2+(-1/5)^2`

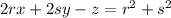
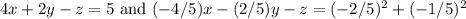
Answer: 4x + 2y - z = 5 and 4x + 2y + 5z = -1

Let's check two points on the line are in our planes, (0,2,-1), (1,0,-1)

Looks good.