Question

On a date when the earth was 147.4x106 km from the sun, a spacecraft parked in a 200 km altitude circular earth orbit was launched directly into an elliptical orbit around the sun with perihelion of 120x106km and aphelion equal to the earth’s distance from the sun on the launch date. Calculate the ∆V required and V[infinity] of the departure hyperbola.

Answer 1

ΔV =
`=v_(p) -v_(c) = 3.337 (km)/(s)`

Step-by-step explanation:

Distance of earth from sun =
`R_(2) = 147.4 * 106 Km`

Spacecraft perihelion =
`R_(2) = 120*106Km`

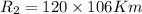
gravitational parameters are now given as

`\mu_(sun) = 132.7* 10^(9)`

`\mu_(earth) = 398600`

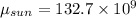
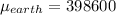
radius of earth = 6378 Km

Heliocentric spacecraft velocity at earth sphere of influence =

`V_(D)^(v) =\sqrt{2\mu_(sun)} \sqrt{(R_(2) )/(R_(1)(R_(1) +R_(2) ) ) }`

`V_(D)^(v) =28.43(km)/(s)`

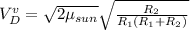
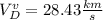
Heliocentric velocity of earth =
`v_(earth) = 30.06(km)/(sec)`

`V_(infinity)= v_(earth)-V_(D)^(v) =30.06-28.43=1.57g(km)/(s)`

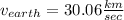
assume

`r_(p) =r_(earth) +r_(altitude) =6378 + 200 = 6578Km`

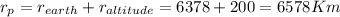
Geometric spacecraft velocity of spacecraft at perigee of departure hyperbola

`v_(p)=\sqrt{v^(2) _(infinity)+(2\mu_(earth) )/(r_(p) ) } = 11.12(km)/(s)`

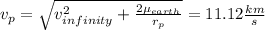
geometric space craft velocity in its circular parking orbit

`v_(c)=\sqrt{(\mu_(earth) )/(r_(p) ) }  = 7.784 (km)/(s)`

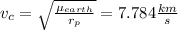
ΔV =
`=v_(p) -v_(c) = 3.337 (km)/(s)`