Question

An ore sample weighs 17.50 N in air. When the sample is suspended by a light cord and totally immersed in water, the tension in the cord is 11.20 N. Find the total volume and the density of the sample.

Answer 1

Volume of the sample: approximately
`\rm 0.6422 \; L = 6.422 * 10^(-4) \; m^(3)`.

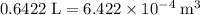Average density of the sample: approximately
`\rm 2.77\; g \cdot cm^(3) = 2.778 * 10^(3)\; kg \cdot m^(3)`.

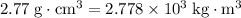Assumption:

• 
  `\rm g = 9.81\; N \cdot kg^(-1)`.
• 
  `\rho(\text{water}) = \rm  1.000* 10^(3)\; kg \cdot m^(-3)`.
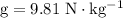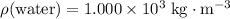• Volume of the cord is negligible.

Step-by-step explanation:

Total volume of the sample

The size of the buoyant force is equal to
`\rm 17.50 - 11.20 = 6.30\; N`.

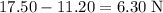That's also equal to the weight (weight,
`m \cdot g`) of water that the object displaces. To find the mass of water displaced from its weight, divide weight with
`g`.

`\displaystyle m = (m\cdot g)/(g) = \rm (6.30\; N)/(9.81\; N \cdot kg^(-1)) \approx 0.642\; kg`.

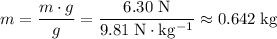Assume that the density of water is
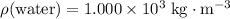`\rho(\text{water}) = \rm  1.000* 10^(3)\; kg \cdot m^(-3)`. To the volume of water displaced from its mass, divide mass with density
`\rho(\text{water})`.

`\displaystyle V(\text{water displaced}) = (m)/(\rho) = \rm (0.642\; kg)/(1.000* 10^(3)\; kg \cdot m^(-3)) \approx 6.42201 * 10^(-4)\; m^(3)`.

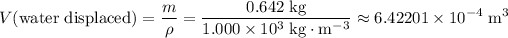Assume that the volume of the cord is negligible. Since the sample is fully-immersed in water, its volume should be the same as the volume of water it displaces.

`V(\text{sample}) = V(\text{water displaced}) \approx \rm 6.422* 10^(-4)\; m^(3)`.

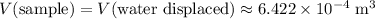Average Density of the sample

Average density is equal to mass over volume.

To find the mass of the sample from its weight, divide with
`g`.

`\displaystyle m = (m \cdot g)/(g) = \rm (17.50\; N)/(9.81\; N \cdot kg^(-1)) \approx 1.78389 \; kg`.

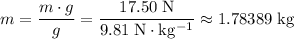The volume of the sample is found in the previous part.

Divide mass with volume to find the average density.

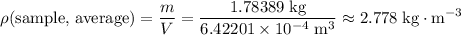`\displaystyle \rho(\text{sample, average}) = (m)/(V) = \rm (1.78389\; kg)/(6.42201 * 10^(-4)\; m^(3)) \approx 2.778\; kg \cdot m^(-3)`.