Question

In a carnival ride, passengers stand with their backs against the wall of a cylinder. The cylinder is set into rotation and the floor is lowered away from the passengers, but they remain stuck against the wall of the cylinder. For a cylinder with a 2.0-m radius, what is the minimum speed that the passengers can have so they do not fall if the coefficient of static friction between the passengers and the wall is 0.25?

Answer 1

v = 8.9 m/s

Step-by-step explanation:

1. f = mg

2. f=цn

3. mg=цn=цmv²/r

v=√(gr/ц)

v=√[(9.8 x 2) ÷ 0.25]

v=8.9 m/s

Answer 2

Minimum speed will be equal to 2.213 m/sec

Step-by-step explanation:

We have given radius of the r = 2 m

Coefficient of friction
`\mu =0.25`

At minimum speed frictional force will be equal to centripetal force

So
`\mu mg=(mv^2)/(r)`

`(v^2)/(r)=\mu g`

`v=√(\mu rg)=√(0.25* 2* 9.8)=2.213m/sec`

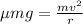
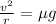
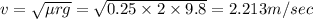
So the minimum speed will be equal to 2.213 m/sec