Answer:
There were 40 pounds of coffee in stock when the trend began.
The number of pounds of coffee in stock decreased by 9% each hour since the trend began.
Explanation:
We are given the following information in the question:
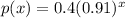
where p(x) models the number of pounds of coffee in hundreds of pounds where x represents the number of hours since the trend has been observed.
When x = 0
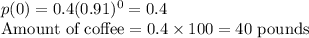
Thus, we can say there were 40 pounds of coffee in stock when the trend began.
When x = 1, that is 1 hour after the trend began. The decrease in coffee is given by:

Percentage decrease =
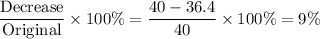
Thus, we can say, the number of pounds of coffee in stock decreased by 9% each hour since the trend began.