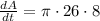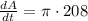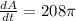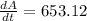Answer:
The area of the pool increasing at the rate of 653.12
 when the radius is 13 cm
when the radius is 13 cm
Explanation:
Given:
radius of the pool increases at a rate of 8 cm/min
To Find:
How fast is the area of the pool increasing when the radius is 13 cm ?
Solution:
we are given with the circular pool
hence the area of the circular pool =
A =
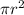 -----------------------------(1)
-----------------------------(1)
The area of the pool os increasing at the rate of 8 cm/min, meaning that the arae of the pool is changing with respect to time t
so differentiating eq (1) with respect to t , we have
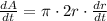
we have to find
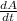 with
with
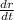 = 8 cm/min and r = 13cm
= 8 cm/min and r = 13cm
substituting the values