Answer:
We would face a rather close decision and switch to α = .01 for a more powerful test.
Explanation:
We are given the following in the question:
Population mean, μ = 40 hours
Sample mean,
 = 37.8 hours
= 37.8 hours
Sample size, n = 108
Alpha, α = 0.05
Sample standard deviation, s = 5.4 hours
First, we design the null and the alternate hypothesis
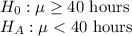
We use one-tailed t test to perform this hypothesis.
Formula:

Putting all the values, we have
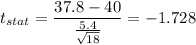
Now,
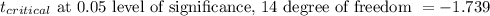
Since,
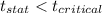
We fail to reject the null hypothesis and accept the null hypothesis. Thus, we conclude that alkaline batteries last at least 40 hours on average in a certain type of portable CD player.
But we faced a close decision. By decreasing alpha we could get stronger results. We would switch to α = .01 for a more powerful test.