Question

Doubly ionized lithium Li2+ (Z = 3) and triply ionized beryllium Be3+ (Z = 4) each emit a line spectrum. For a certain series of lines in the lithium spectrum, the shortest wavelength is 40.5 nm. For the same series of lines in the beryllium spectrum, what is the shortest wavelength?

Answer 1

tex]\lambda_{Be}[/tex] = 22.78 nm

Step-by-step explanation:

Bohr's model for the hydrogen atom has been used by other atoms with a single electric charge by changing the number of charges by the charge of the new atom (atomic number)

`E_(n)`= k e² / 2a₀ (1 /n²)

ao = h'² / k m e² h' = h/2πi

For another atom with a single electron in the last layer

a₀ ’= h’² / k m (Ze)²

a₀ ’= a₀ / Z²

Therefore, when replacing in the equation

`E_(n)` = - Z² Eo/n²

E₀ = 13,606 eV

The transition occurs when the electron stops from one level to another

`E_(n)` -
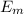`E_(m)` = Z² E₀ (1 / n² - 1 / m²) = Z² ΔE

Let's relate this expression to the wavelength

c = λ f

E = h f

E = h c /λ

h c / λ = Z² ΔE

λ = 1 / Z² (hc / ΔE)

λ = 1 / Z² λ_hydrogen

Let's apply this last equation to our case

Lithium Z = 3

`E_(n)` = - 9 Eo / n²

40.5 10-9 = 1/9 λ_hydrogen

Beryllium Z = 4

λ = 1/16 λ_hydrogen

Let's write our two equations is and solve

40.5 10-9 = 1/9 λ_hydrogen

tex]\lambda_{Be}[/tex] = 1/ 16 λ_hydrogen

40.5 10⁻⁹ = 1/9 (16
`\lambda_(Be)` )

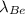tex]\lambda_{Be}[/tex] = 40.5 9/16

tex]\lambda_{Be}[/tex] = 22.78 nm