Question

It is reasonable to model the number of winter storms in a season as with a Poisson random variable. Suppose that in a good year the average number of storms is 4, and that in a bad year the average is 5. If the probability that next year will be a good year is 0.6 and the probability that it will be bad is 0.4, find the expected value and variance in the number of storms that will occur.

Answer 1

E(A)= E[E(A|B)]= 4*0.6 +5*0.4 =4.4

Var(A)= E[Var(A|B)] +Var[E(X|Y)]]=4.4+19.6=24

Explanation:

Previous concepts

The Poisson process is useful when we want to analyze the probability of ocurrence of an event in a time specified. The probability distribution for a random variable X following the Poisson distribution is given by:

`P(X=x) =\lambda^x (e^(-\lambda))/(x!)`

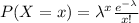
For this distribution the expected value is the same parameter
`\lambda`

`E(X)=\mu =\lambda`

Other equations useful:

Let X and Y random variables

E(X) =E[E(X|Y)] (conditional expectation)

Var(X)=E[Var(X|Y)]+Var[E(X|Y)] (Total variance)

Solution to the problem

Let A the random variable that represent the number of winter storms next year

B a binary variable, B=1 if the next year is a good year and B=0 in the other case. Then we have this:

E(A|B=1) = 4 and E(A|B=0)=5

We can use the propoerties of conditional expectation like this:

E(A)= E[E(A|B)]= E(A|B=1)P(B=1) +E(A|B=0)P(B=0)

E(A)= E[E(A|B)]= 4*0.6 +5*0.4 =4.4

And we can use also the properties for conditional variance we have the following values:

Var(A|B=1)=4 Var(A|B=0)=5, by the propertis of the Poisson distribution

And then the conditional variance is givne by:

`Var[E(A|B)]= E(A|B=1)^2 P(B=1) +E(A|B=0)^2 P(B=0)`

And if we replace we got:

`Var[E(A|B)]= 4^2 *0.6 +5^2 *0.4 =19.6`

And we have also that the expected value for the conditional variance is given by:

E[Var(A|B)]= 4*0.6 +5*0.4 =4.4

And then finally the variance for the random variable A is given by:

Var(A)= E[Var(A|B)] +Var[E(X|Y)]]=4.4+19.6=24