Question

Tickets for a high school dance cost $1.00 each of purchased in advance of the dance, but $1.50 each if bought at the door. If 100 tickets were sold and $120 was collected, how many tickets were sold in advance and how many were sold at the door?

Answer 1

Tickets were sold in advance are 60 and the tickets were sold at the door are 40.

Explanation:

Given:

Tickets for a high school dance.

Cost $1.00 each of purchased in advance of the dance.

Cost $1.50 each if bought at the door.

100 tickets were sold and $120 was collected.

Now, to find the tickets that were sold in advance and sold at the door.

Let the number of tickets sold in advance be
`x`.

And the number of tickets sold at the door be
`y`.

So, the total number of tickets sold:

`x+y=100.`

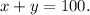
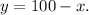`y=100-x.`......(1)

Now, the total amount collected:

`1.00x+1.50y=120.`

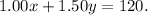
Putting the equation (1) in the place of
`y` we get:

`1x+1.5(100-x)=120`

`1x+150-1.5x=120`

`150-0.5x=120`

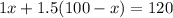
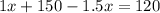
Adding both sides by
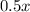`0.5x` we get:

`150=120+0.5x`

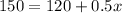
Subtracting both sides by 120 we get:

`30=0.5x`

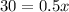
Dividing 0.5 by both sides we get:

`60=x`

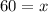
Thus, the number of tickets sold in advance = 60.

Putting the value of
`x` in equation (1) we get:

`y=100-60`

`y=40.`

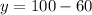
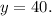
So, the number of tickets sold at the door = 40.

Therefore, tickets were sold in advance are 60 and tickets were sold at the door are 40.