Answer:
Length of ladder = 45.30 ft
Explanation:
Given data:
Distance between the bottom of the ladder and side of house = 14 ft
Angle of elevation of the ladder = 72°
To find length of the ladder.
From the data given to us we can construct a right triangle ABC.
For the Δ ABC
AC= 14 ft
∠A= 72°
We can apply trigonometric ratio to find side AB which is the length of the ladder.
 [ ∵
[ ∵
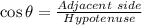 ]
]
Multiplying both sides by AB.
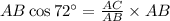
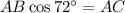
Dividing both sides by cos72°
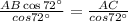

Substituting value of AC and cos 72°
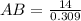
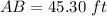
Thus, length of the ladder = 45.30 ft