Question

Are two lines parallel, perpendicular or neither 3x+7y=15 and 7x-3y=6

Answer 1

The lines are perpendicular

Explanation:

we know that

If two lines are parallel, then their slopes are equal

If two lines are perpendicular, then their slopes are opposite reciprocal (the product of their slopes is equal to -1)

we have

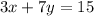`3x+7y=15` ----> equation A

isolate the variable y

`7y=-3x+15`

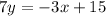
Divide by 7 both sides

`y=-(3)/(7)x+(15)/(7)`

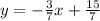
The slope of the line A is
`m_A=-(3)/(7)`

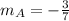
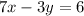`7x-3y=6` ----> equation B

isolate the variable y

`3y=7x-6`

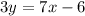
Divide by 3 both sides

`y=(7)/(3)x-2`

The slope of the line B is
`m_B=(7)/(3)`

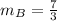
Compare the slope of both lines

`m_A=-(3)/(7)`

`m_B=(7)/(3)`

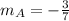
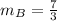
so

`m_A \\eq m_B` ----> the lines are not parallel

Find the product of the slopes

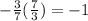`-(3)/(7)((7)/(3))=-1` ----> the lines are perpendicular