Question

Suppose 8.41 moles of a monatomic ideal gas expand adiabatically, and its temperature decreases from 395 to 279 K. Determine (a) the work done (including the algebraic sign) by the gas, and (b) the change in its internal energy.

Answer 1

a) W=12166.20876 J

b) U= -12166.20876 J

Step-by-step explanation:

No. of moles, n = 8.41

Change of temperature, ΔT = T1 - T2

= 395 - 279

= 116 K

For monatomic gas, γ = 5/3

γ -1 = 2 /3

Solution:

(a)

Work done,
`W= (nR)/(\gamma-1)(T_1-T_2)`

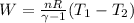
plugging values we get

`W= (8.314*8.41)/(2/3)(116)`

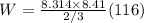
Ans: 12166.20876 J

Work done, W = + 12166.20876 J

(b)

From first law of thermodynamics, dQ = U + W

but, dQ = 0 ( adiabatic process)

Hence, U = - W

= - 12166.20876 J

Ans:

Change in internal energy, U = - 12166.20876 J