Question

Line w and line v are perpendicular to each other. Line w passes through the points ( -4,8 ) and ( 12,-2 ). What is the slope of line v?

Answer 1

The slope of line "v" is
`(8)/(5)`

Solution:

Given that Line w and line v are perpendicular to each other

Also given that line w passes through the points ( -4, 8 ) and ( 12, -2 )

To find: slope of line v

Since line w and line v are perpendicular to each other, product of slopes of line w and line v are equal to -1

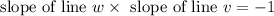`\text {slope of line } w * \text { slope of line } v=-1` ---- eqn 1

Let us first find slope of line w

The slope "m" of a line is given as:

`m=(y_(2)-y_(1))/(x_(2)-x_(1))`

`\text {Here } x_(1)=-4 \text { and } x_(2)=12 \text { and } y_(1)=8 \text { and } y_(2)=-2`

`m=(-2-8)/(12-(-4))=(-10)/(16)=(-5)/(8)`

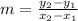
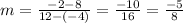
Thus the slope of line "w" is
`(-5)/(8)`

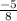
Substituting the slope of w in eqn 1 we get,

`\begin{array}{l}{(-5)/(8) * \text { slope of line } v=-1} \\\\ {\text { slope of line } v=(8)/(-5) *-1=(8)/(5)}\end{array}`

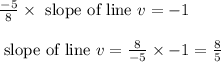
Thus the slope of line "v" is
`(8)/(5)`