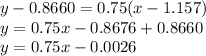Question

Find an equation for the line tangent to the curve at the point defined by the given value of t.​ Also, find the value of StartFraction d squared y Over dx squared EndFraction d2y dx2 at this point. x equals=sec t ​, y equals=cos t​; tequals= pi Over 6

Answer 1

a) 3x + 4y = 4√3

b)
`(d^(2)y )/(dx^(2) ) = (3√(3) )/(4)`

Explanation:

a) x = sec t

y = cos t

t = π/6

dy/dt = -sin t

dx/dt = sect tant = (1/cost) * (sint /cost)

dx/dt = sint/cos²t

`dy/dx = (dy/dt )/(dx/dt)`

dy/dx = -sint * cos²t/sint

dy/dx = - cos²t

At t = π/6

dy/dx = - cos²(π/6) = -3/4

x = sec(π/6) = 2/√3

y = cos(π/6) = √3/2

The slope, m = dy/de

Equation of the tangent line is:

`y - y_(1) = m(x - x_(1) )`

At t = π/6

`y - (√(3) )/(2) = (-3)/(4) (x - (2)/(√(3) ) )`

By simplifying the equation above, the equation for the tangent line becomes:

3x + 4y = 4√3

b) Find the value of
`(d^(2)y )/(dx^(2) )` at t = π/6

`y = cost = 1/sect`

since
`x = sect`

y = 1/x

`dy/dx = (-1)/(x^(2) )`

`(d^(2)y )/(dx^(2) ) = (2)/(x^(3) ) \\(d^(2)y )/(dx^(2) ) = (2)/(sec^(3)t )`

At t = π,6, sect = 2/√3

`(d^(2)y )/(dx^(2) ) = (2)/((2/√(2)) ^(3))\\(d^(2)y )/(dx^(2) ) = (3√(3) )/(4)`

Answer 2

`y = 0.75x-0.0026`

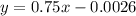
Explanation:

Given that a function is parametrized as

`x=sect \\y = cost`

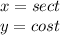
we have to find the equation of the line tangent at

`t=(\pi)/(6)`

First let us find the point of contact by substituting values of t

`x=sec (\pi)/(6) = 1.157\\y = cos (\pi)/(6)=0.8660`}

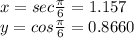Now let us find derivatives
`dx=sect tant dt\\dy = -sint dt\\(dy)/(dx) =(-sint)/(sect tant)\\=-0.75`

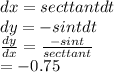
Slope = 0.75 and one point = (1.157, 0.8660)

Using point slope formula we find equation of tangentline is

`y-0.8660 = 0.75(x-1.157)\\y = 0.75x-0.8676+0.8660\\y = 0.75x-0.0026`