Question

A 80 W light bulb (normally run at 120 V) is attached to a transformer. The voltage source in the transformer is 65 V and Np = 30. How many turns does the secondary coil need to be to run this light bulb at 120 W?

Answer 1

67.8 turns needed by the secondary coil to run the bulb.

Step-by-step explanation:

We know that,

`\text { Electric power }(p)=(V^(2))/(R)`

`\text { Hence, } (P_(1))/(P_(2))=(V_(1)^(2) / R)/(V_(2)^(2) / R)`

`(P_(1))/(P_(2))=(V_(1)^(2))/(V_(2)^(2))`

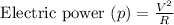
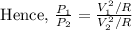
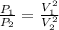
For calculating number of turns

`(N_(P))/(N_(S))=(V_(P))/(V_(S))`

Given that,

`80 \mathrm{W}\left(P_(1)\right) \text { bulb with voltage } 120 \mathrm{V}\left(V_(1)\right) \text { is connected to a transformer. }`

`\text { The source voltage of a transformer is }\left(V_(P)\right) \text { is } 65 \mathrm{V}`

`\text { The number of turns in primary winding of transformer is }\left(N_(P)\right) \text { is } 30 .`

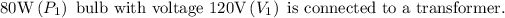
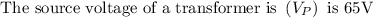
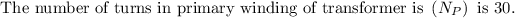
We need to find the number of turns in the secondary winding
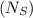`\left(N_(S)\right)` to run the bulb at 120W
`\left(P_(2)\right)`

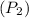
Firstly find the secondary voltage in the transformer use,
`(P_(1))/(P_(2))=(V_(1)^(2))/(V_(2)^(2))`

`(80)/(120)=(120^(2))/(V_(2)^(2))`

`V_(2)^(2)=(120^(2) * 120)/(80)`

`V_(2)^(2)=(1728000)/(80)`

`V_(2)^(2)=21600`

`V_(2)=√(21600)`

`V_(2)=146.9 \mathrm{V}=V_(S)`

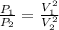
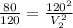
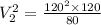
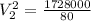
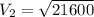
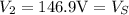
Now, finding the number of turns in secondary coil. Use,
`(N_(P))/(N_(S))=(V_(P))/(V_(S))`

`(30)/(N_(S))=(65)/(146.9)`

`N_(S)=(30 * 146.9)/(65)`

`N_(S)=(4407)/(65)`
`N_(S)=67.8`

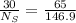
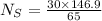
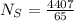
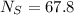
The number of turns in the secondary winding are 67.8 turns.