Question

A lake polluted by bacteria is treated with an antibacterial chemical. Aftertdays, thenumber N of bacteria per milliliter of water is approximated byN(t) = 20(t12−ln(t12))+ 30for 1≤t≤15.a. When will the number of bacteria be a minimum?b. What is the minimum number of bacteria during this time?c. When will the number of bacteria be a maximum?d. What is the maximum number of bacteria during this time?

Answer 1

N(1)=50 is a minimum

N(15)=4391.7 is a maximum

Explanation:

Extrema values of functions

If the first and second derivative of a function f exists, then f'(a)=0 will produce values for a called critical points. If a is a critical point and f''(a) is negative, then x=a is a local maximum, if f''(a) is positive, then x=a is a local minimum.

We are given a function (corrected)

`N(t) = 20(t^2-lnt^2)+ 30`

`N(t) = 20(t^2-2lnt)+ 30`

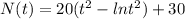
(a)

First, we take its derivative

`N'(t) = 20(2t-(2)/(t))`

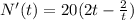
Solve N'(t)=0

`20(2t-(2)/(t))=0`

Simplifying

`2t^2-2=0`

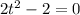
Solving for t

`t=1\ ,t=-1`

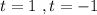
Only t=1 belongs to the valid interval
`1\leqslant t\leqslant 15`

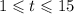
Taking the second derivative

`N''(t) = 20(2+(2)/(t^2))`

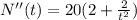
Which is always positive, so t=1 is a minimum

(b)

`N(1)=20(1^2-2ln1)+ 30`

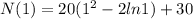
N(1)=50 is a minimum

(c) Since no local maximum can be found, we test for the endpoints. t=1 was already determined as a minimum, we take t=15

(d)

`N(15)=20(15^2-2ln15)+ 30`

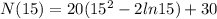
N(15)=4391.7 is a maximum