Answer:
Velocity of the helium nuleus = 1.44x10⁴m/s
Velocity of the proton = 2.16x10⁴m/s
Step-by-step explanation:
From the conservation of linear momentum of the proton collision with the He nucleus:
![P_(1i) + P_(2i) = P_(1f) + P_{2f]](https://img.qammunity.org/2020/formulas/physics/college/1nduzqeozw2md0s9hi0taanccf8v0hvna9.png) (1)
(1)
where
 : is the proton linear momentum initial,
: is the proton linear momentum initial,
 : is the helium nucleus linear momentum initial,
: is the helium nucleus linear momentum initial,
 : is the proton linear momentum final,
: is the proton linear momentum final,
 : is the helium nucleus linear momentum final
: is the helium nucleus linear momentum final
From (1):
 (2)
(2)
where m₁ and m₂: are the proton and helium mass, respectively,
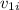 and
and
 : are the proton and helium nucleus velocities, respectively, before the collision, and
: are the proton and helium nucleus velocities, respectively, before the collision, and
 and
and
 : are the proton and helium nucleus velocities, respectively, after the collision
: are the proton and helium nucleus velocities, respectively, after the collision
By conservation of energy, we have:
 (3)
(3)
where
 and
and
 : are the kinetic energy for the proton and helium, respectively, before the colission, and
: are the kinetic energy for the proton and helium, respectively, before the colission, and
 and
and
 : are the kinetic energy for the proton and helium, respectively, after the colission
: are the kinetic energy for the proton and helium, respectively, after the colission
From (3):
 (4)
(4)
Now we have two equations: (2) ad (4), and two incognits:
 and
and
 .
.
Solving equation (2) for
 , we have:
, we have:
 (5)
(5)
From getting (5) into (4) we can obtain the
 :
:

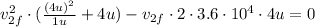
From solving the quadratic equation, we can calculate the velocity of the helium nucleus after the collision:
 (6)
(6)
Now, by introducing (6) into (5) we get the proton velocity after the collision:
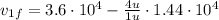
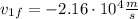
The negative sign means that the proton is moving in the opposite direction after the collision.
I hope it helps you!