Question

In the function f(x)=x^2 has the domain of {-2,4,8,9} what is the range

Answer 1

For the function f(x) = x^2 range will be { 4 , 16 , 68 , 81 }

Solution:

Given that:

`\text {Function is } f(x)=x^(2)`

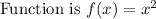
Domain of the function is {-2, 4, 8, 9}

Need to determine range of the function.

Domain of the function is possible input of the function that is x and range of the function is possible output of the function that is f(x)

As there are only four input values for x that are -2,4,8,9 we can determine the range by calculating value of f(x) for each of the x

`\begin{array}{l}{\text {At } x=-2:} \\\\ {f(x)=f(-2)=-2^(2)=4}\end{array}`

`\begin{array}{l}{\text {At } x=4:} \\\\ {f(x)=f(4)=4^(2)=16}\end{array}`

`\begin{array}{l}{\text {At } x=8:} \\\\ {f(x)=f(8)=8^(2)=64} \\\\ {\text {At } x=9:} \\\\ {f(x)=f(9)=9^(2)=81}\end{array}`

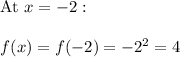
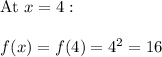
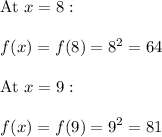
Thus the range of given function is { 4 , 16 , 68 , 81 }