Answer:
Differentiation of both the term is
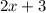
Explanation:
As we have to use first principle of derivatives lets recall the formula.
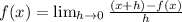
Solving our eqaution.
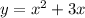
We will work with
 then
then
 separately then put in the above formula.
separately then put in the above formula.
1.
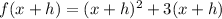
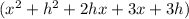
Now

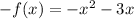
Plugging the values of both.
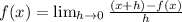
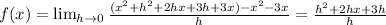
Taking
 as common.
as common.

Putting
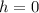
Then
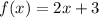 is the final derivative.
is the final derivative.
This will be same for
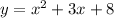 as we have to put
as we have to put
 only.
only.
2.
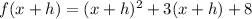
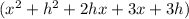
Then
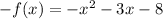
Plugging the values of both.
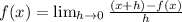

Taking
 as common.
as common.

Putting
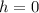
Then
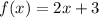 is the final derivative.
is the final derivative.
So both the derivatives are same.