Question

A (10.0+A) g ice cube at -15.0oC is placed in (125+B) g of water at 48.0oC.

Find the final temperature of the system when equilibrium is reached.

Ignore the heat capacity of the container and assume this is in a calorimeter, i.e. the system is thermally insulated from the surroundings.

Give your answer in oC with 3 significant figures.

Answer 1

This thermodynamics question in Physics involves calculating the final temperature when an ice cube is placed in water, using energy conservation. The process includes raising the temperature of the ice to 0°C, melting the ice, and then using remaining energy to warm the water or melt more ice, depending on the energy available. Exact calculations require specific masses for the ice cube and water.

Step-by-step explanation:

The subject of this question lies within the field of Physics, specifically within the area of thermodynamics involving calorimetry. To calculate the final temperature of a system consisting of an ice cube placed in water, we use the principle of conservation of energy. This principle stipulates that energy lost by the warmer body (the water) is equal to the energy gained by the colder body (the ice cube).

First, we bring the ice cube to 0°C by calculating the energy required to raise the temperature of ice from -15.0°C to 0°C. Then, we use the heat of fusion to determine the energy necessary to melt the ice. Next, the water's temperature drop is calculated based on the amount of energy absorbed by the ice during heating and melting. If there is enough energy to melt all of the ice, then additional thermal energy from the water will raise the temperature of the resulting liquid water until thermal equilibrium is reached. If there is not enough energy to melt all the ice, the final temperature will be 0°C.

Without specific values for A and B (the masses of the ice cube and the water), a numeric solution cannot be provided. However, the process described is general and applicable to any specific masses once provided.

Answer 2

`T_(f)` = 38.0° C

Step-by-step explanation:

The thermal transfer processes are governed by two equations one for there is a change of state, during this process the temperature does not change and another for which there is a change of temperature.

Q = ± m L

Q = m
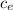`c_(e)` ΔT

In calorimetric processes the heat transferred is equal to the heat absorbed by the system

-Qc = Qabs

Let's apply these equations to our system, we will assume the quantity A and B zero, reduce the magnitudes to the SI system

m1 = 10 g = 0.010 kg

m2 = 125 g = 0.125 kg

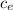`c_(e)` (ice) = 2090 J / kg ºC

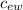`c_(ew)` (water) = 4186 J / kg ºC

Lf = 3.33 105 J / kg

Let's write the expression for the heat given

Qc = m₂
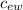`c_(ew)` (T₀ -
`T_(f)` )

Qc = 0.125 4186 (48.0 -
`T_(f)`)

Qc = 523.25 (48.0 -
`T_(f)`)

The expression for absorbed is

Qabs = Q1 + Q2 + Q3

calculate Q₁

Q₁ = m
`c_(e)` (
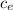`T_(f)` - T₀)

Q₁ = 0.010 2090 (0 - (-15.0))

Q₁ = 313.5 J

Let's change state from ice to liquid water

Q₂ = + mL

Q₂ = 0.010 3.33 105

Q₂ = 3.33 103 J

Now let's heat the liquid water to the equilibrium temperature

Q₃ = m₁
`c_(ew)` (
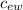`T_(f)`-T₀)

Q₃ = 0.01 4186 (
`T_(f)` - 0)

Q₃ = 41.86
`T_(f)`

let's calculate the maximum heat assigned

Qc = 0.125 4186 (48.0 - 0)

Qc = 2.5 104 J

Qc> (Q₂ + Q₁)

all the ice is melted

523.25 (48.0 -
`T_(f)`) = Q1 + Q2 + 41.86
`T_(f)`

(41.86 +523.25)
`T_(f)`= 523.25 48 - Q1 -Q2

565.11
`T_(f)` = 25116 - 313.5 - 3.33 103

`T_(f)` = 21469.5 / 565.11

`T_(f)` = 38.0 ° C