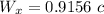Question

In an "atom smasher," two particles collide head on at relativistic speeds. If the velocity of the first particle is 0.741c to the left, and the velocity of the second particle is 0.543c to the right (both as measured in the lab rest frame), how fast are the particles moving with respect to each other?

Answer 1

`W_x = 0.9156\ c`

Step-by-step explanation:

given,

velocity of particle 1 = 0.741 c to left

velocity of second particle = 0.543 c to right

relative velocity between the particle = ?

for the relative velocity calculation we have formula

`W_x = (|u_x - v_x|)/(1-(u_xv_x)/(c^2))`

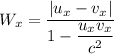
u_x = 0.543 c

v_x = - 0.741 c

`W_x = (0.543 c - (-0.741 c))/(1-((0.543 c)(-0.741 c))/(c^2))`

`W_x = (0.543 c +0.741 c))/(1+((0.543)(0.741)c^2)/(c^2))`

`W_x = (1.284c)/(1+0.402363)`

`W_x = 0.9156\ c`

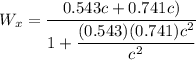
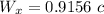
Relative velocity of the particle is
`W_x = 0.9156\ c`