Answer:
Mean =
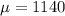
Standard deviation =
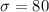
Find the probabilities for the average length of life of the selected batteries.
A)The average is between 1128 and 1140.
We are supposed to fidn P(1128<x<1140)
Formula :

At x = 1128
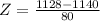

Refer the z table for p value
P(x<1128)=0.4404
At x = 1140
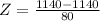
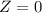
Refer the z table for p value
P(x<1140)=0.5
So,P(1128<x<1140)=P(x<1140)-P(x<1128)=0.5-0.4404=0.0596
Hence the probabilities for the average length of life of the selected batteries is between 1128 and 1140 is 0.0596
B)The average is greater than 1152.
P(x>1152)
At x = 1128


Refer the z table for p value
P(x<1152)=0.5596
So,P(x>1152)=1-P(x<1152)=1-0.5596=0.4404
Hence the probabilities for the average length of life of the selected batteries is greater than 1152 is 0.4404
C) The average is less than 940.
P(x<940)
At x = 940
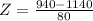
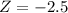
Refer the z table for p value
P(x<940)=0.5596
Hence the probabilities for the average length of life of the selected batteries is less than 940 is 0.5596