Question

what would be the time of flight, maxiumum height and horizontal range of the football was kicked from the floor? if a field goal attempt was made from 40 yards (36.58 m) and the goal post is 10 feet tall (3.084 m) will the kicker make the field goal?

Answer 1

time of flight T= 5.77sec

maxiumum height h max= 66.78m

horizontal range S=50.91m

Step-by-step explanation:

Assume that the footaball moves with the initial velocity= Vo=40m/s

and angle
`\alpha`=
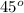`45^(o)`(for maximum range)

Given that,

the distance from place of attempting goal to goal post =d= 36.58m

height of goal post=3.084m

For projectile motion, time of flight T is,

T=
`(2Vi sin\alpha )/(g)` =
`(2(40) sin 45^(o) )/(9.8)`

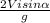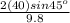
T= 5.77sec

According to second equation of motion

S=Vot+ 1/2 gt^2

S= h max, Vo= vertical component of velocity= 40sin 45=28.28

t=average time= (time of flight +0 )/2= 3.6/2=1.8sec

h max= 28.28*1.8+ 1/2(9.8)(1.8)^2

h max= 66.78m

For horizontal range,

S= v*t

v= horizontal component of velocity= Vocos45=40cos 45 = 28.28

t=average time= (time of flight +0 )/2= 3.6/2=1.8sec

S= 28.28*1.8

S=50.91m

Answer 2

Answers:

a) 3.511 s

b) 15.1062 m

c) 86.281 m

Step-by-step explanation:

Assuming the initial velocity of the ball is
`V_(o)=30 m/s` and the angle
`\theta=30\°`, we have the following data:

`d=40 yards=36.58 m` the distance between the football player and the the goal post

`H=10 ft=3.084 m` the height of the goal post

Now, this can be solved with the following equations related to parabolic motion:

`t_(flight)=(2V_(o) sin \theta)/(g)` (1)

`y_(max)=y_(o)+V_(o)sin \theta (t_(flight))/(2)-(g)/(2)((t_(flight))/(2))^(2)` (2)

`x=V_(o)cos\theta t_(flight)` (3)

Where:

`t_(flight)` is the time of flight

`g=9.8 m/s^(2)` is the acceleration due gravity

`y_(max)` is the maximum height, when the time is half the time of flight
`t_(flight)`

`y_(o)=0 m` is the initial height

`x` is the horizontal range

Knowing this, let's begin with the answers:

a) Time of flight

We will use equation (1):

`t_(flight)=(2(30 m/s) sin(30\°))/(9.8 m/s^(2))` (4)

`t_(flight)=3.511 s` (5)

b) Maximum height

In this case, we have to use equation (2) and substitute the
`t_(flight)` calculated in (5):

`y_(max)=(30 m/s) sin(30\°) (3.511 s)/(2)-(9.8 m/s^(2))/(2)((3.511 s)/(2))^(2)` (6)

`y_(max)=15.1062 m` (7)

c) Horizontal range

Let's use equation (3):

`x=(30m/s)cos(30\°) (3.511 s)` (8)

`x=86.281 m` (9)

Since the maximum height and the horizontal range of the ball are greater than
`d` and
`H`, we can say the kicker is able to make the field goal.