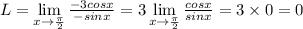Using L' Hopital's rule, find the limit of \lim_{x \to (\pi )/(2) } 3secx-3tanx

Question

Using L' Hopital's rule, find the limit of


`\lim_{x \to (\pi )/(2) } 3secx-3tanx`

Answer 1

L=0

Explanation:

`L=\lim\limits_{x \rightarrow (\pi)/(2)}3secx-3tanx`

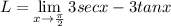
Replacing the value of x we get ∞ - ∞ which is an indetermined expression

We must transform the limit so it can be shown as a fraction and the L'Hopital's rule can be applied:

`L=\lim\limits_{x \rightarrow (\pi)/(2)}(3-3sinx)/(cosx)=(0)/(0)`

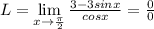
Now we can take the derivative in both parts of the fraction

`L=\lim\limits_{x \rightarrow (\pi)/(2)}(-3cosx)/(-sinx)=3\lim\limits_{x \rightarrow (\pi)/(2)}(cosx)/(sinx)=3* 0=0`