Question

Let production be given by P = bLαK1−α where b and α are positive and α < 1. If the cost of a unit of labor is m and the cost of a unit of capital is n, and the company can spend only p dollars as its total budget, then maximizing the production P is subject to the constraint mL + nK = p. Show that the maximum production occurs when L=αp/m and K=(1-α)p/n.

Answer 1

The proof is completed below

Explanation:

1) Definition of info given

We have the function that we want to maximize given by (1)

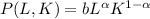`P(L,K)=bL^(\alpha)K^(1-\alpha)` (1)

And the constraint is given by
`mL+nK=p`

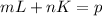
2) Methodology to solve the problem

On this case in order to maximize the function on equation (1) we need to calculate the partial derivates respect to L and K, since we have two variables.

Then we can use the method of Lagrange multipliers and solve a system of equations. Since that is the appropiate method when we want to maximize a function with more than 1 variable.

The final step will be obtain the values K and L that maximizes the function

3) Calculate the partial derivates

Computing the derivates respect to L and K produce this:

`(dP)/(dL)=b\alphaL^(\alpha-1)K^(1-\alpha)`

`(dP)/(dK)=b(1-\alpha)L^(\alpha)K^(-\alpha)`

4) Apply the method of lagrange multipliers

Using this method we have this system of equations:

`(dP)/(dL)=\lambda m`

`(dP)/(dK)=\lambda n`

`mL+nK=p`

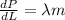
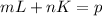
And replacing what we got for the partial derivates we got:

`b\alphaL^(\alpha-1)K^(1-\alpha)=\lambda m` (2)

`b(1-\alpha)L^(\alpha)K^(-\alpha)=\lambda n` (3)

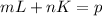`mL+nK=p` (4)

Now we can cancel the Lagrange multiplier
`\lambda` with equations (2) and (3), dividing these equations:

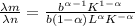`(\lambda m)/(\lambda n)=(b\alphaL^(\alpha-1)K^(1-\alpha))/(b(1-\alpha)L^(\alpha)K^(-\alpha))` (4)

And simplyfing equation (4) we got:

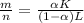`(m)/(n)=(\alpha K)/((1-\alpha)L)` (5)

4) Solve for L and K

We can cross multiply equation (5) and we got

`\alpha Kn=m(1-\alpha)L`

And we can set up this last equation equal to 0

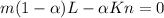`m(1-\alpha)L-\alpha Kn=0` (6)

Now we can set up the following system of equations:

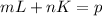`mL+nK=p` (a)

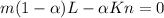`m(1-\alpha)L-\alpha Kn=0` (b)

We can mutltiply the equation (a) by
`\alpha` on both sides and add the result to equation (b) and we got:

`Lm=\alpha p`

And we can solve for L on this case:

`L=(\alpha p)/(m)`

And now in order to obtain K we can replace the result obtained for L into equations (a) or (b), replacing into equation (a)

`m((\alpha P)/(m))+nK=p`

`\alpha P +nK=P`

`nK=P(1-\alpha)`

`K=(P(1-\alpha))/(n)`

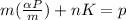
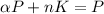
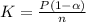
With this we have completed the proof.