Question

Suppose a random sample of n = 25 observations is selected from a population that is normally distributed with mean equal to 103 and standard deviation equal to 13. (a) Give the mean and the standard deviation of the sampling distribution of the sample mean x. (Enter your standard deviation to two decimal places.)

Answer 1

`\mu_x=103\\\sigma_x=2.6`

Explanation:

For any random variable x,

We know that the mean and the standard deviation of the sampling distribution of the sample mean x is given by :-

`\mu_x=\mu\\\\\sigma_x=(\sigma)/(√(n))`

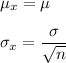
, where n = sample size.

`\mu`= population mean

`\sigma`= population standard deviation equal.

Given : n=25

`\mu=103`

`\sigma=13`

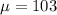
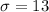
Then , the mean and the standard deviation of the sampling distribution of the sample mean x will be :-

`\mu_x=\mu=103\\\\\sigma_x=(\sigma)/(√(n))\\\\=(13)/(√(25))\\\\=(13)/(5)=2.6`

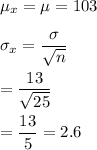
Hence, the mean and the standard deviation of the sampling distribution of the sample mean x :

`\mu_x=103\\\sigma_x=2.6`