Question

For a particular flight from Dulles to SF, an airline uses wide-body jets with a capacity of 460 passengers. It costs the airline $4,000 plus $60 per passenger to operate each flight. Through experience the airline has discovered that if a ticket price is $T, then they can expect (460−1.T) passengers to book the flight. Determine the ticket price, T, that will maximize the airline's profit.

Answer 1

Answer:$ 260

Explanation:

Given

Initially 460 passenger travels

It cost $ 4000 +$60 per passenger

If ticket Price is $ T

then they expect 460-T passengers

Total Revenue generated by tickets
`=T* (460-T)`

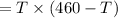
cost to airlines
`=4000+60* (460-T)`

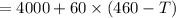
Profit is
`=T* (460-T)-4000-60* (460-T)`

`P=(460-T)(T-60)-4000`

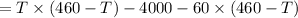
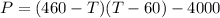
To get maximum Profit differentiate P w.r.t to T and Equate it to zero

`\frac{\mathrm{d} P}{\mathrm{d} T}=\frac{\mathrm{d} }{\mathrm{d} (460-T)(T-60)T}-0`

`\frac{\mathrm{d} P}{\mathrm{d} T}=-T+60+460-T=0`

`520=2T`

`T=260`

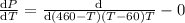
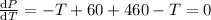
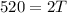
Therefore it cost $ 260 to get maximum Profit