Question

In a random sample of 64 audited estate tax​ returns, it was determined that the mean amount of additional tax owed was ​$3489 with a standard deviation of ​$2595.

Construct and interpret a​ 90% confidence interval for the mean additional amount of tax owed for estate tax returns.
1) The lower bound is ​$?
2) The upper bound is $?

Answer 1

Answer with explanation:

Formula for confidence interval for population mean ( if population standard deviation is unknown ) :

`\overline{x}\pm t_(\alpha/2)(s)/(√(n))`

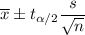
, where n= sample size

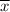`\overline{x}` = sample mean

s= sample standard deviation

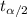`t_(\alpha/2)` = two-tailed t-value for significance level of (
`\alpha`).

Let x denotes the amount of additional tax owed .

We assume that amount of additional tax owed is normally distributed .

As per given , we have

n= 64

Degree of freedom : df = 63 [ df= n-1]

`\overline{x}=\$3489`

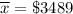
s= $2595

`\alph=1-0.90=0.1`

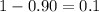
Using t-distribution table ,

`t_(\alpha/2, df)= t_(0.05, 63)= 1.6694`

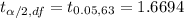
Then , 90% confidence interval for the mean additional amount of tax owed for estate tax returns would be :

`\$3489\pm (1.6694)(2595)/(√(64))\\\\\$3489\pm\$541.51\\\\ =($3489-\$541.51, $3489+\$541.51)=(\$2947.49,\ $4030.51)`

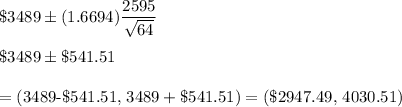
1) The lower bound is ​$2947.49 .

2) The upper bound is $4030.51 .

Interpretation : We are 90% confident that the true population mean amount of additional tax owed lies between $2947.49 and $4030.51.